Quantum computing has the potential to be one of the defining technologies of the 21st century, with practical applications that could completely transform modern society. Despite its enormous significance, most people have absolutely no idea what quantum computing is.
In this article, we’re going to explain what quantum computers are and give a brief introduction to how they work. You don’t need a background in science to follow along, just a few minutes of spare time and a desire to learn.
What’s the definition?
A quantum computer is a device that uses the principles of quantum mechanics to perform certain calculations much faster than a regular computer. When we say faster, we don’t mean that scientists will spend less time waiting around for their results. A future large-scale quantum computer could solve problems that would take millions of years on today’s best supercomputers (1,2).
These problems aren’t just abstract maths puzzles, they’re real-world challenges that will have a massive impact on people’s lives. Quantum simulations of chemical reactions would enable the discovery of life-saving medicines, advanced materials, and sustainable manufacturing processes (3–5). Quantum algorithms could lead to breakthroughs in artificial intelligence, while quantum cryptography could provide unbreakable data encryption secured by the laws of physics[1] (6,7). The significance of these applications has led to a lot of hype around quantum computing, eagerly fed by companies in the industry looking to secure customers and raise funding. To cut through this hype and understand the underlying technology, we need to look at some fundamental physics.
What is Quantum Mechanics?
The basis of quantum computing is quantum mechanics, which is a scientific theory that describes the behaviour of the basic building blocks of our universe, like atoms, electrons, and photons[2]. Let’s quickly define two important terms: a “quantum system”is something whose behaviour can be explained through quantum mechanics, and a “quantum state” is the mathematical description of a quantum system.
The key principles of quantum mechanics that you’ll need to understand quantum computing are entanglement, interference, and superposition:
Entanglement: When a group of particles are entangled, measuring one of them instantly causes a change[3] in the others, even if they are vast distances apart. In technical terms, the quantum states of entangled particles can’t be described independently of one another.
Entanglement doesn’t exist in our large-scale everyday world, so it can be hard to wrap your head around it. As an example, imagine that we had a pair of entangled quantum coins, which each exist as a combination of heads and tails at the same time until we measure them[4] (I never said it would be a good example). If I flipped one of the coins and it landed on heads, then I could know with 100% certainty that yours would be tails before you’d flipped it. The instant its entangled partner was measured, your coin was in the state tails, instead of the combination of heads and tails it was the moment before.
Interference: Interference is a phenomenon where overlapping waves combine or cancel out. It’s how noise-cancelling headphones work: they emit sound waves that interfere destructively with background noise. A simple diagram of destructive interference is shown below:
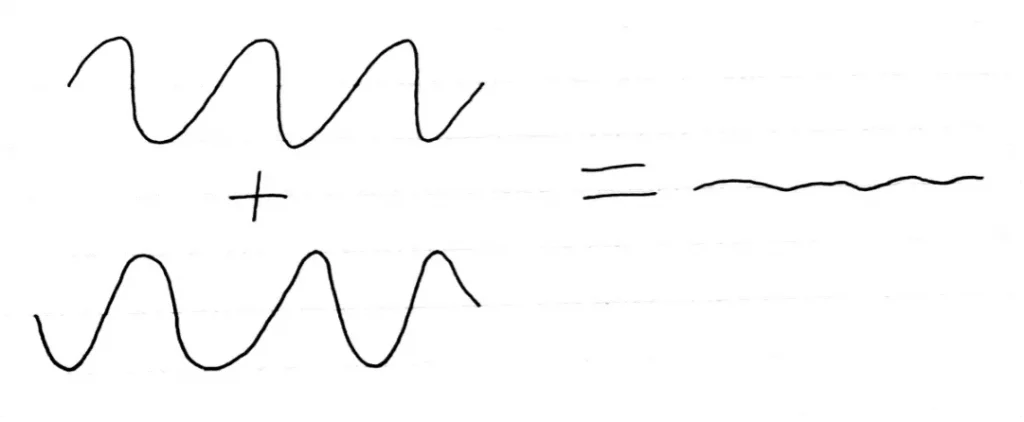
Quantum particles can act like waves, so they experience quantum interference. The maths describing quantum interference is a bit different to regular interference, but the general idea is the same.
Superposition: A quantum state can be described mathematically as the sum of other quantum states. This is another similarity between quantum states and waves, which can be described as the sum of other waves. The quantum coin existing as a combination of heads and tails in our entanglement example was in a superposition of heads and tails.
Quantum mechanics is one of the most stunningly accurate scientific theories in history, but an engineer would never use it to design a car or a bridge. Instead, they’d use the rules from a less precise group of theories known as classical physics.
Classical physics is a set of approximations and simplified rules used to describe the stuff we interact with every day (heat, sound, motion, gravity, etc.). These are the laws of physics you probably studied in school. When many quantum objects interact, it becomes easier to describe their collective behaviour using classical physics rather than quantum mechanics. A football is made of atoms, but you don’t need quantum physics to predict what will happen if you kick it. “Classical” in this context refers to the non-quantum, large-scale, everyday world of footballs and kicking that we live in.
To explain how quantum computers use entanglement, interference and superposition to perform calculations, we’re going to examine qubits: the fundamental components of (most[5]) quantum computers.
What is a Qubit?
A classical computer like the device you’re reading this on uses bits to represent information. A bit can have a value of 0 or 1, like a switch that is either on or off. Modern computers are made of billions of these tiny switches, allowing them to perform complex tasks such as delivering your daily meme supply. For instance, the word “Hi” is stored in a computer (using ASCII binary code) as 1001000 1101001. As well as storing information, computers perform calculations using bits: 2 + 2 = 4 is represented in binary as 10 + 10 = 100.
The quantum version of a bit is called a qubit. Physically, a qubit is just a two-level quantum system. One example of a qubit is a photon that can be sent down either of two optical fibres. An optical fibre is a wire made of flexible glass or plastic that reflects photons internally. It can be used to transport light like copper wire carries electricity.
If the photon is in the first of the two fibres, then the qubit is in the state |0>. If the photon is in the second fibre, then the qubit is in the state |1>. When you measure the state of this qubit by detecting where the photon is, you’ll get a classical 0 or 1. This is shown in the diagram below:
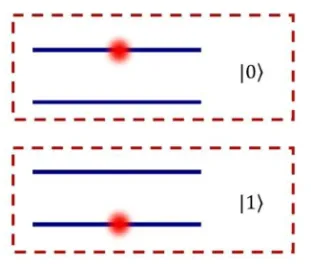
Quick note: |x> is how we write a quantum state in Dirac notation, which is a convention that makes quantum physics calculations easier.
One of the weird features of quantum mechanics is that a single photon can be sent down both fibres at the same time, as a superposition of the two states. Measuring the photon causes the superposition to collapse, and the photon will be found in one fibre or the other. Qubits existing in a superposition is one of the key differences between quantum and classical computing, which will be discussed further in the next article of this series.
How do we use this for calculations?
A qubit-based quantum computer is generally composed of three stages:
1. Initialisation: The qubits are given a known value when the calculation starts, such as every qubit being in the state.
2. Manipulation: A quantum circuit uses interference and entanglement to apply mathematical operations to the qubits.
3. Measurement: The quantum states of the qubits are measured to read the results of the calculation.
An example of this structure can be seen in the following diagram of a photonic quantum computer:
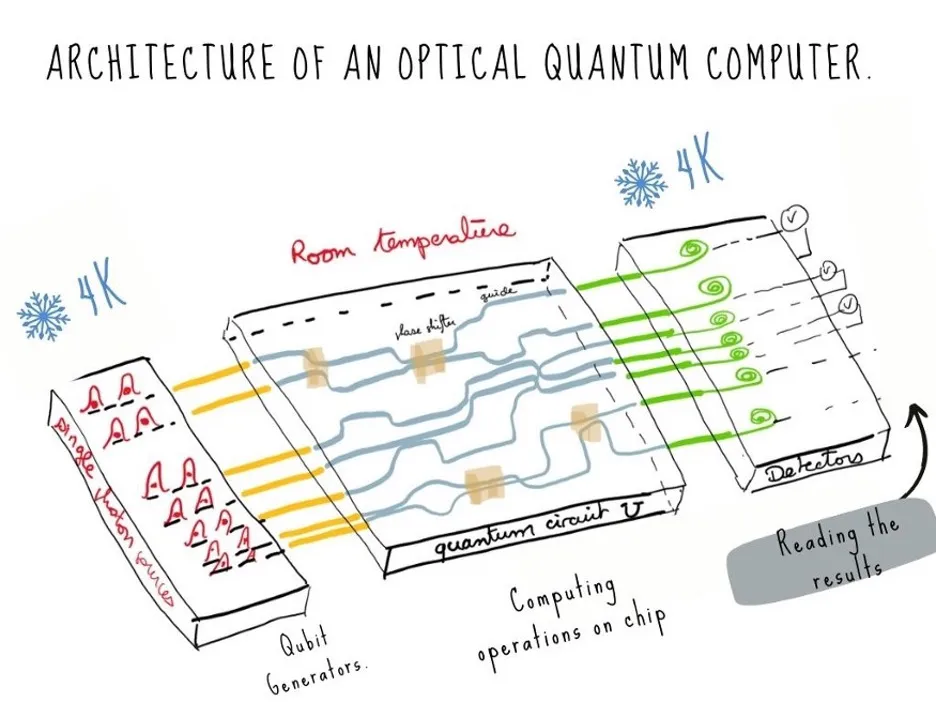
At the end of a calculation, the qubits in a quantum computer exist in a superposition of all the possible outcomes. When you measure the qubits, you collapse this superposition, and get one of the possible outcomes at random as your answer. Quantum algorithms can be designed so that the quantum states in the superposition corresponding to the wrong answers interfere destructively and cancel out, leaving behind only the right answers. Entanglement is used to connect qubit superpositions together to perform useful calculations.
By running the circuit and measuring the qubits hundreds or thousands of times, we can build a graph of how likely each of the possible outcomes are. This graph (a probability distribution) is the final result of our quantum calculation.
The process of manipulating probabilities with superposition, interference, and entanglement is fundamentally different to how normal computers operate. That is why quantum computers can do certain tasks so quickly: they’re not better than classical computers in general, they just work differently. Quantum computers are much better suited to mundane supercomputer-style tasks like designing medicines than crucial everyday tasks like posting memes, so they are expected to co-exist with classical computers rather than replacing them entirely. Many of the most famous quantum algorithms actually use a combination of quantum and classical techniques to solve problems[6].
What’s next?
Hopefully this explanation has given you a basic understanding of what a quantum computer is. In the next article in this series, we’re going to examine how a quantum computer works in more detail, hopefully without getting lost in technical jargon.
If you are interested to find out more about our technology, our solutions or job opportunities visit quandela.com
Footnotes:
1. Optical quantum communications can provide data protection through security protocols such as BB84, while quantum computers will be able to factor large numbers using Shor’s Algorithm and break modern RSA encryption. There are, however, non-quantum encryption techniques that are immune to Shor’s algorithm.
2. Atoms are not elementary particles like quarks and gluons, but they are still small enough to be described with quantum mechanics. Quantum mechanics is also needed to explain certain behaviours of some large-scale objects like black holes and neutron stars.
3. Entanglement is a slippery subject. Technically change occurs in the quantum states of the other particles; i.e. their mathematical descriptions. An important side point is that the change is not directly observable, except through clever strategies which involve comparisons of observations on each particle. If the changes were directly observable it would provide a means of instantaneous (faster-than-light) communication across great distances — something that’s already disallowed by relativity, one of our other great theories of physics.
4. Maybe you could begin to wonder at this point whether this combination of heads or tails is really all that strange… After all I could perform a coin flip, close my fist around it to catch it, and until I open it again I won’t know if it’s a head or a tail. That’s a kind of combination of heads and tails too, right? Well, yes, but this is where everyday and quantum coins begin to differ. The everyday coin really is just one or the other, and all that’s really happening is that I’m ignorant and don’t have the information about which one it is yet. On the other hand, a quantum coin can really be in a superposition of both heads and tails. And we can know that it’s in a genuine superposition by doing clever experiments that look for interference effects.
5. Photonic quantum computers can demonstrate quantum advantage using a technique called Boson Sampling without encoding information as qubits. We will explain this in detail in a future article.
6. Some examples of quantum-classical algorithms include Shor’s Algorithm (8), VQE (9), and QAOA (10).
References
1. Arute F, Arya K, Babbush R, Bacon D, Bardin JC, Barends R, et al. Quantum supremacy using a programmable superconducting processor. Nature. 2019 Oct;574(7779):505–10.
2. Madsen LS, Laudenbach F, Askarani MFalamarzi, Rortais F, Vincent T, Bulmer JFF, et al. Quantum computational advantage with a programmable photonic processor. Nature. 2022 Jun 2;606(7912):75–81.
3. Kirsopp JJM, Di Paola C, Manrique DZ, Krompiec M, Greene-Diniz G, Guba W, et al. Quantum Computational Quantification of Protein-Ligand Interactions [Internet]. arXiv; 2021 [cited 2022 Jul 19]. Available from: http://arxiv.org/abs/2110.08163
4. Clinton L, Cubitt T, Flynn B, Gambetta FM, Klassen J, Montanaro A, et al. Towards near-term quantum simulation of materials [Internet]. arXiv; 2022 [cited 2022 Jun 24]. Available from: http://arxiv.org/abs/2205.15256
5. Greene-Diniz G, Manrique DZ, Sennane W, Magnin Y, Shishenina E, Cordier P, et al. Modelling Carbon Capture on Metal-Organic Frameworks with Quantum Computing [Internet]. arXiv; 2022 [cited 2022 May 17]. Available from: http://arxiv.org/abs/2203.15546
6. Havlicek V, Córcoles AD, Temme K, Harrow AW, Kandala A, Chow JM, et al. Supervised learning with quantum enhanced feature spaces. Nature. 2019 Mar;567(7747):209–12.
7. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing. Theor Comput Sci. 1984 Dec;560:7–11.
8. Shor PW. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J Comput. 1997 Oct;26(5):1484–509.
9. Peruzzo A, McClean J, Shadbolt P, Yung MH, Zhou XQ, Love PJ, et al. A variational eigenvalue solver on a quantum processor. Nat Commun. 2014 Sep;5(1):4213.
10. Farhi E, Goldstone J, Gutmann S. A Quantum Approximate Optimization Algorithm [Internet]. arXiv; 2014 [cited 2022 Jul 20]. Available from: http://arxiv.org/abs/1411.4028






