What is randomness?
What is randomness? And how can we generate it? Both questions — the first mathematical, the second technological — have profound implications in many of today’s industries and our everyday lives.
Imagine that we wanted to make a random list of 0s and 1s. This list could be used to protect your medical records as a keyword, could ensure that a lottery is trustworthy, or could encrypt a digital letter to your long-lost half-step-brother-in-law. To make this list, maybe you use the classic coin-flip method: write down a 1 every time the coin lands heads-up and a 0 otherwise. Or maybe, instead, you time the decay of the radioactive cesium that you stole from the lab. Is one of these methods better than the other; does it even matter? Yes, on both counts.
Let’s explore the principles of randomness together, and some new results from Quandela that generate certifiable randomness according to the laws of quantum mechanics.
Generating randomness
We’ve already talked about two Random-Number Generators (RNGs), the coin flip and the radioactive cesium, both of which are examples of true RNGs. That is, they rely on unpredictable physical processes (or, rather, not-easily-predictable) to make their lists of 0s and 1s. But there are many kinds of RNGs, which you can see in Fig. 1
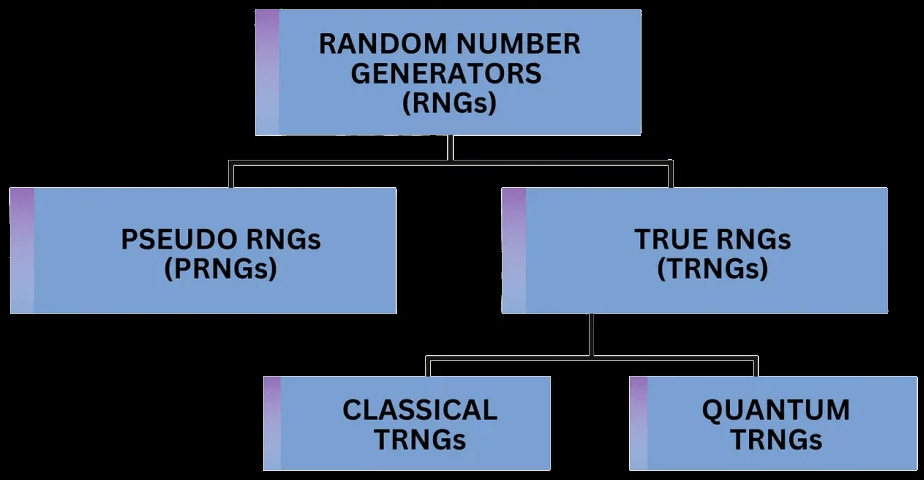
The one programmers are probably most familiar with is pseudo-RNGs. Here, you give a random seed number to a mathematical algorithm, which uses that number to deterministically generate a longer list of numbers that look random. While this is a convenient way to generate random numbers, there is a big caveat: if someone ever gained access to your seed numbers, past or present, they could replicate all of your numbers for themselves!
Then you have true RNGs, of which there are two main kinds: classical and quantum. These are based on unpredictable physical processes. A simple example of a classical true RNG is the coin flip, but there are many more complex methods that are used in modern electronics, for example measuring thermal noise from a resistor. The Achille’s heel of classical true RNGs is that while the details of the generating process may be unknown, they are still in principle knowable. What are the implications of this? Well, if a bad guy wants to know your random numbers, they can always build a better model of your classical system for better predictions. Your classical RNG must therefore necessarily be complex.
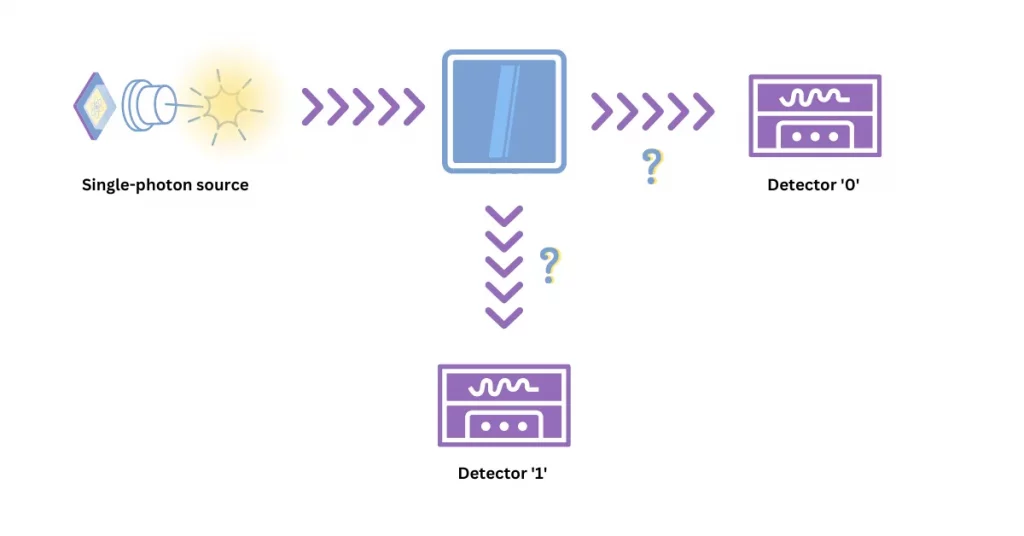
Quantum true RNGs can do better. Rather than watching our stolen cesium beta-decay, we’ll take an example from quantum optics (see Fig. 2). Here, a train of single photons is shone onto a semi-transparent mirror, which has two outputs. Because quantum mechanics is inherently unpredictable, the single photon will randomly take one of these two paths, after which it can be measured by one of two detectors, which correspond to 0 or 1. This is good at first sight, but be careful: in an ideal world, where all of the photons really are single, the beam splitter doesn’t absorb any photons, and the detectors don’t have any noise or loss, then we really do get independent and identically distributed random numbers. But this is not an ideal world, and so we call this kind of quantum RNG device-dependent because we must trust the physical engineering of the RNG. However, quantum RNGs are still a step in the right direction because we do not have to complexify them like in the classical case.
Now, we wouldn’t have given the previous example a fancy name like device-dependent quantum true random number generator if there wasn’t also such a thing as device-independent quantum RNGs — the holy grail of RNGs. The latter devices can generate and validate their own random numbers: they are certifiably random, independent of the underlying hardware. But how can we make such a thing? We use entanglement.
Essentially, if Alice and Bob share two entangled particles, and Alice measures her particle, then the state of Bob’s particle is instantly changed according to Alice’s measurement, no matter how far apart they are. This is a fundamentally quantum effect which cannot be described classically. But we have to be careful that Alice and Bob aren’t cheating. If Alice and Bob are physically too close, then we don’t know if they’re secretly sharing information to coordinate their measurements. When they’re sufficiently separated, we call this nonlocality.
So, if Alice and Bob create a pair of entangled particles, then randomly choose how to measure them, the outcomes of their measurements are quantum-certified random so long as satisfy the nonlocality condition (and a couple of other secondary conditions which are beyond the scope of this article; see Quandela’s recent publication on quantum RNGs).
Because of nonlocality, these kinds of random-number experiments tend to be big so that the measurements are far, far apart. In a world which is both obsessed with small, scalable devices and also maximum security, how can one reconcile this paradox? This is exactly the problem that researchers at Quandela have solved.
Quandela’s contributions
They ask:
‘ How can we certify randomness generation in a device-independent way with a practical small-scale device, where [Alice and Bob could cheat thanks to communication] between the physical components of the device? ’
Put another way, when you have a small device that might normally allow Alice and Bob to cheat by communicating information before the other one measures their particle, can you account for this local communication somehow to still generate certified random numbers? Quandela’s protocol measures the amount of information that an eavesdropper could potentially use to fake violation of locality, and then sets a bound on how well the device should perform if it is to still produce certified random numbers. The device also periodically tests itself to validate these numbers.
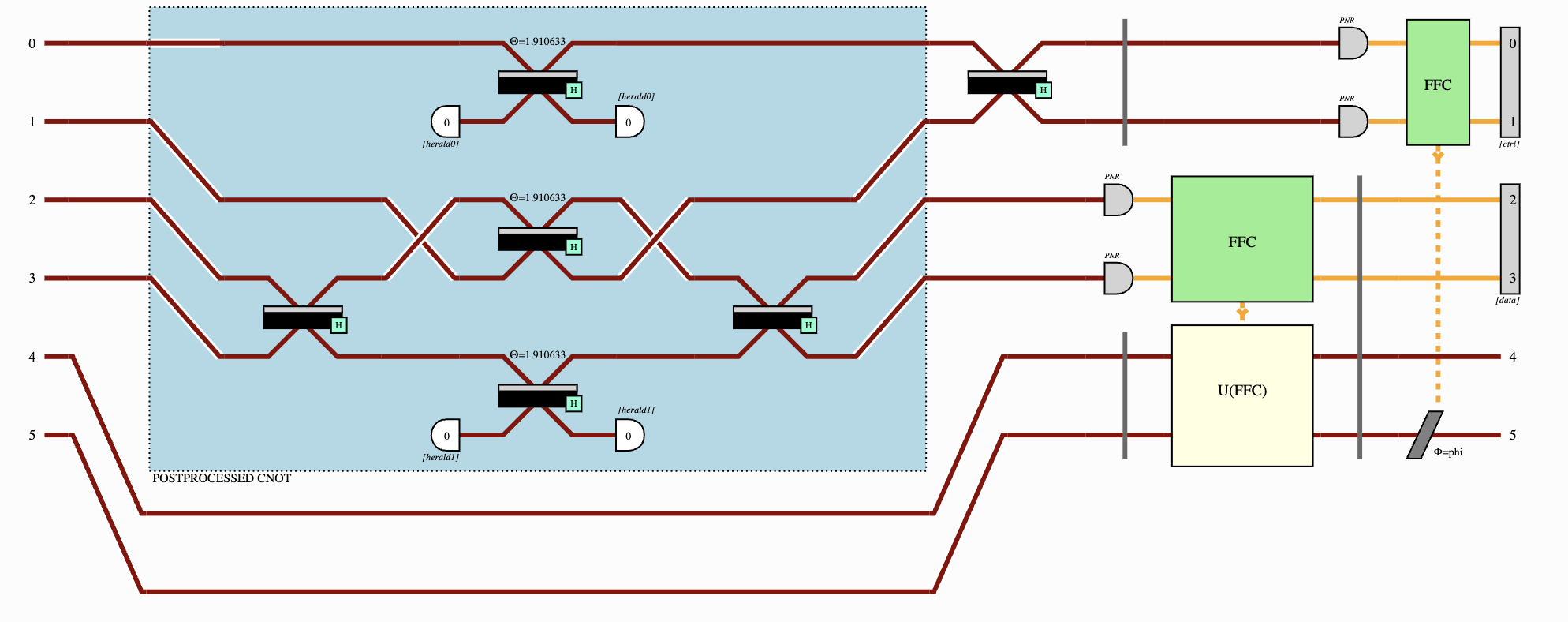
And not only has Quandela derived the theory, but they’ve also demonstrated it experimentally on a two-qubit photonic chip using Quandela’s patented single-photon quantum dot source, show in Fig. 3.

If this all sounds like a big deal, that’s because it is — the technical details are all found in the recent publication, with a patent on its way!
This achievement represents a major step towards building real-world, useable quantum-certified random number generators, one more tool in Quandela’s arsenal of quantum technologies.