As quantum processors scale, they will need to be connected through photonic links. Photons are the only practical carriers of quantum information beyond the local chip: they are fast, can travel long distances, and preserve coherence even at room temperature. This vision of distributed quantum computing makes it essential to accurately model the gates and protocols that rely on photons to connect distant qubits.
Accurate simulation is a critical step toward building such systems. It allows researchers to optimize hardware design, test new quantum control strategies, and anticipate the impact of real-world imperfections such as noise or photon loss. Without fast, reliable tools, progress would rely heavily on costly trial-and-error experiments.
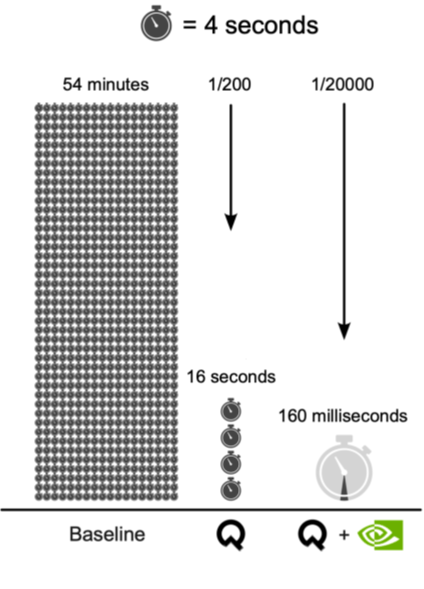
Recently, Quandela and NVIDIA achieved a breakthrough in this direction: by combining Quandela’s Zero-Photon Generator (ZPG) method with CUDA-Q’s new SuperOperator API and batched Liouvillian evolution, simulations of photon-mediated spin–spin gates were accelerated by up to 20,000x compared to standard approaches. This turns what was once an hour-long computation into a real-time task on a single GPU (see Figure 1).
In the sections below, we describe the steps that make this possible: from the challenges of simulating quantum light-matter interactions, to the ZPG reformulation that removes exponential scaling, to the CUDA-Q features that unlock massive GPU acceleration. We finish with benchmarks and physical results that highlight how this approach opens the door to simulation of distributed quantum gates.
Light–matter interaction
The challenge with simulating photon-mediated operations is that when a matter qubit evolves in time, it emits a multi-mode wavepacket of light rather than a simple single-mode photon. When several such wavepackets interfere and are measured, the resulting feedback on the matter qubits becomes extremely complex to capture accurately.
Standard approaches try to address this by:
- Simulating how the qubit and its photon transition evolve locally.
- Computing how the light and matter become correlated during emission.
- Integrating those correlations over time to model what detectors would see.
The problem is that each extra photon adds a new dimension of integration. For two or more photons, the cost grows rapidly and soon becomes a major bottleneck. On top of that, the coupled nature of the integrals makes it very hard to use GPUs efficiently.
Reformulating the problem
To overcome the exponential slowdown of standard approaches, Quandela developed the Zero-Photon Generator (ZPG) method [1]. Instead of evaluating multi-dimensional correlation integrals, ZPG reformulates the dynamics as a set of independent master equations that can be solved in parallel. This eliminates the need for expensive nested time integrations and makes the workload naturally suited for GPU acceleration.
The starting point is the master equation for the system density matrix \(p(t)\):
$$\frac{d}{dt}\rho(t) = \mathcal{L}[\rho(t)]$$
where \(\mathcal{L}\) is the Liouvillian superoperator that combines both the Hamiltonian dynamics and dissipative terms associated with photon emission.
To model detection events, we introduce collapse operators \(C_m\) for each detected mode \(m\) These collapse operators are unitary mixtures of transition operators of the system. The ZPG method modifies the Liouvillian into a “tilted” version that weights these jumps by virtual detector efficiencies \(\eta_m\):
$$\frac{d}{dt}\rho(t;\boldsymbol{\eta})=\mathcal{L}[\rho(t;\boldsymbol{\eta})]-\sum_{m}\eta_mC_m\rho(t;\boldsymbol{\eta})C^{\dagger}_m$$
Evolving the system under many carefully chosen values of \(\eta_m\) generates a compact representation of all possible detection outcomes. The actual detection probabilities and full quantum process map (Choi matrices) can then be recovered by applying an inverse Fourier transform over the variables \(\eta_m\).
In practice, this replaces one difficult multi-dimensional integral with many smaller, independent equations that can be solved side by side — a structure that maps directly onto GPU batching in CUDA-Q.
Computing with CUDA-Q
CUDA-Q is NVIDIA’s open-source platform for quantum simulation and algorithm development [2]. It is designed to take advantage of GPU acceleration while fitting naturally into HPC workflows. For open quantum systems, CUDA-Q recently release version 0.12 with two new features that are particularly well suited to the ZPG method:
- A SuperOperator API, which makes it possible to construct custom Liouvillians directly from Hamiltonians, dissipators, and detector collapse operators.
- Batched evolution, which allows many Liouvillians to be evolved in parallel on the GPU.
Together, these capabilities let us translate the tilted master equations from ZPG directly into efficient GPU workloads.
The SuperOperator API provides building blocks for assembling the effective dynamics of a light-matter system. For example, one can write down the Hamiltonian part and add dissipators and extra jump terms in just a few lines:
from cudaq import SuperOperator
L = SuperOperator.left_multiply(-1j * H)
L += SuperOperator.right_multiply(1j * H)
for (S, Sd) in transition_operators:
L = SuperOperator.left_right_multiply(S, Sd)
L += SuperOperator.left_multiply(-0.5 * Sd * S)
L += SuperOperator.right_multiply(-0.5 * Sd * S)
for (C, Cd), eta in zip(collapse_operators, eta_list):
L += SuperOperator.left_right_multiply(-eta * C, Cd)Once the Liouvillian terms are defined, CUDA-Q makes it possible to evolve a whole family of them for a set of \(\eta_m\) in parallel. This batched evolution is useful not only for ZPG, but for any setting where many slightly different open-system trajectories must be compared, such as noise averaging or parameter sweeps. This can be accomplished by simply passing a list of Liouvillian superoperators to the cudaq.evolve() function:
from cudaq import evolve
solutions = evolve([L1, L2, L3, L4], dimensions=dims, schedule=schedule, initial_state=rho0)With these two features, the many independent tilted equations that arise in ZPG become a natural fit for GPU acceleration. Instead of evolving each equation one by one, CUDA-Q computes the entire set on the GPU in a single batched job. This is what enables orders-of-magnitude improvements in runtime, turning previously intractable simulations into real-time computations.
Application: the remote RUS CZ gate
A central challenge for distributed quantum computing is how to entangle qubits that are physically far apart. A standard approach is to generate spin–photon entangled pairs at each node, and then interfere the photons on a beam splitter. By measuring the photons jointly, we can probabilistically entangle the remote spins.
In the most direct version of this protocol, when the measurement succeeds, the two spins are projected into an entangled state. However, when the measurement fails, the effect is equivalent to having indirectly measured the spins themselves, which destroys the quantum information.
This limitation can be overcome by carefully choosing the measurement basis. By inserting Hadamard gates on the photons, and performing the Bell measurement in a mutually unbiased basis, the protocol changes character:
- A success corresponds to applying a teleported controlled-Z (CZ) gate between the remote spins.
- A failure, instead of projecting the spins, simply implements the identity operation (up to known local phase corrections).
This modified scheme is known as a Repeat-Until-Success (RUS) gate [3], since failed attempts leave the qubits intact, allowing the process to be retried until the entangling gate is achieved. Importantly, this property means that what matters is the precise operation applied to the qubits for each possible photon detection outcome, not just the successful one.
Implementation with quantum dots
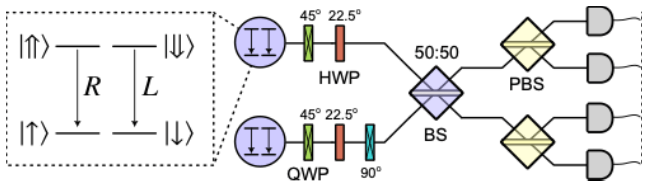
To implement this protocol, we can use a charged quantum dot trion system. In this system, degenerate polarization transitions allow the generation of spin–photon entangled pairs [4]. The emitted photons carry their quantum information in polarization, which can be manipulated using standard linear-optics components such as waveplates, beam splitters, and polarizing beam splitters (see Figure 2).
In practice, the evolution of the spin is not perfect. In quantum dots, one dominant source of noise comes from the quasi-static Overhauser field: random nuclear spin fluctuations that act like a slowly varying magnetic field on the electron spin. When a photon is emitted, this random field slightly shifts the spin precession frequency, effectively introducing an error.
To model the average performance of the remote gate, one must therefore average over an ensemble of Overhauser field configurations. In other words, we compute the gate process for many different noise realizations and take the statistical mean.
Handling with CUDA-Q
This averaging step is another case where CUDA-Q’s batching capability is invaluable. Each Overhauser configuration corresponds to a slightly different Hamiltonian term in the Liouvillian. By constructing a list of such Liouvillians and passing them to cudaq.evolve() in batch mode, we can simulate hundreds of noise realizations in parallel on the GPU.
The result is an efficient way to compute not just the ideal process map of the RUS CZ gate for every photon detection outcome, but also its realistic average fidelity under experimentally relevant noise. This capability is key to validating whether such entangling gates can meet the thresholds required for fault-tolerant distributed quantum computing.
Benchmarking the speedup
To quantify the performance gains, we benchmarked the simulation of the RUS CZ gate under different approaches. As a figure of merit, we computed the average total variation distance (TVD) between the simulated photon detection distributions (obtained by tracing the Choi matrices) and the exact distribution. This provides a direct measure of simulation accuracy.
We compared three approaches:
- Standard time-integrated correlation functions in QuTiP [5].
- The ZPG method implemented in QuTiP.
- The ZPG method implemented in CUDA-Q.
For the CUDA-Q runs, we tested two integrators: a second-order Runge–Kutta (RK2) and a fourth-order Runge–Kutta (RK4). For each method, we measured the wall-clock evaluation time as a function of the accuracy (TVD) achieved (see Figure 3).
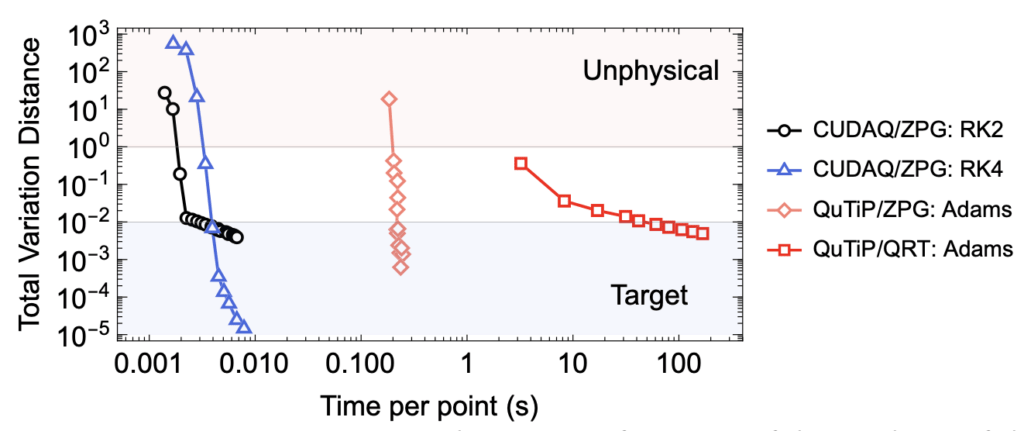
Since it is necessary to average over at least 100 configurations of the Overhauser field, a precision threshold of 0.01 is the minimum to achieve reliable results. However, even with this relatively lenient requirement, the baseline QuTiP correlation-function approach quickly becomes impractical. For four detectors with three outcomes each (a total of 81 possible outcomes), QuTiP requires approximately 40 seconds per outcome—nearly an hour to produce a full Choi matrix decomposition of just one Overhauser configuration and at just two digits of precision.
Implementing ZPG in QuTiP removes the need for multi-time integration and reduces the runtime to about 200 milliseconds per outcome, or roughly 16 seconds for the full decomposition of one Overhauser configuration. With ZPG implemented in CUDA-Q using batched evolution, the acceleration is dramatic: just 2 milliseconds per outcome using RungeKuttaIntegrator(order=2), or 0.16 seconds for a complete 81-outcome Choi matrix decomposition at the same precision.
This corresponds to a performance increase of nearly 20,000x compared to the baseline method, turning what was once an hour-long calculation into a real-time task.
Discussion and outlook
The acceleration achieved with CUDA-Q and the ZPG method does more than make previously intractable simulations possible: it opens the door to entirely new applications. With runtimes reduced to fractions of a second, it becomes feasible to integrate these simulations into machine-learned optimization loops, where control protocols can be adapted in real time while fully accounting for the complex physics of light–matter interactions.
Because the simulator works directly with time-domain dynamics, it can naturally incorporate a wide range of realistic physical effects. These include quantum control pulses, active switching in reconfigurable circuits, phonon-induced dephasing, spectral wandering, multi-photon emission, higher-resolution detectors, photon losses, cavity enhancements, and arbitrary unitary transformations of the photonic modes. The example shown here focused on a time-independent RUS CZ gate protocol, but the same framework applies seamlessly to time-dependent evolutions, where many of these physical effects play a central role.
It is also worth comparing against the fastest time-independent solvers currently available. The Krylov subspace matrix exponential algorithm (as implemented in Expokit and distributed with Mathematica) is an established benchmark for sparse systems. Running the same RUS CZ gate simulation with this solver gave a runtime of 32 milliseconds per outcome—already far faster than QuTiP, but still an order of magnitude slower than CUDA-Q’s batched Runge–Kutta approach on the GPU. This shows that CUDA-Q can outperform even highly optimized commercial solvers, and without the barrier of proprietary software.
Looking forward, there are opportunities to push performance even further. Implementing Krylov subspace methods for sparse, time-independent evolution inside CUDA-Q could combine the best of both approaches. Extending these ideas to piecewise time-dependent dynamics using sequential matrix exponential–vector products (expmv) would further expand the toolkit. For sparse problems such as photon-mediated interactions, this hybrid strategy may eventually surpass even Runge–Kutta solvers.
These advances bring us closer to the practical design of distributed quantum architectures built on photonic links. By making realistic light–matter simulations accessible in real time, CUDA-Q and ZPG provide a foundation for developing and validating the next generation of entangling protocols, control strategies, and hardware components. As quantum processors scale, such tools will be essential for turning the promise of photonic and hybrid quantum computing into a utility-scale reality.
References
[1] S. C. Wein, Simulating photon counting from dynamic quantum emitters by exploiting zero-photon measurements, Phys. Rev. A 109, 023713 (2024).
[2] NVIDIA CUDA-Quantum, https://developer.nvidia.com/cuda-q, https://github.com/NVIDIA/cuda-quantum.
[3] Y.-L. Lim, A. Beige, and L.-C. Kwek, Repeat-until-success linear optics distributed quantum computng, Phys. Rev. Lett. 95, 030505 (2005).
[4] G. de Gliniasty, P. Hilaire, P.-E. Emeriau, S. C. Wein, A. Salavrakos, and S. Mansfield, A spin-optical quantum computing architecture, Quantum 8, 1423 (2024).
[5] N. Lambert et al., QuTiP 5: The quantum toolbox in python, arXiv:2412.04705 (2024).
Implementation details
All CUDA-Q simulations presented here were carried out on a single NVIDIA H100 GPU hosted on Scaleway Cloud. The CUDA-Q version used was v0.12.0, which introduced the SuperOperator API and batched evolve functionality. The implementation of the Zero-Photon Generator (ZPG) method in CUDA-Q, including scripts for reproducing the RUS CZ gate simulation and benchmarks, is available on GitHub: https://github.com/stephenwein/cudaq_applications
The QuTiP-based implementation of ZPG was constructed using the ZPGenerator package also available on GitHub: https://github.com/Quandela/ZPGenerator. The QuTiP time-integration approach was not fully implemented due to the difficulty of constructing the Choi matrix simulation without the ZPG method. Instead, the benchmark was estimated from computing two-time correlation functions with the built-in correlation_3op_2t() function. Both QuTiP benchmarks were run on a single core of a Macbook Pro M2 and the scripts are available on GitHub: https://github.com/stephenwein/cudaq_applications
These resources allow readers to reproduce the benchmarks, explore different noise models, and extend the method to custom photonic circuits or time-dependent control protocols.